懵逼的一天
SX-D1
矩阵乘法
对于两个矩阵,想要进行相乘操作,必须满足其中一个的行数等于另一个的列数,即矩阵(m,p)和矩阵(p,n)相乘为矩阵(m,n)。
如图所示:

扫描线
这是一种做线段树题的思想。如果在题目中的查询操作有单调性,也就是说我们现在查询只用得到这个单调的轴上之前的地方,然后我们就可以把这些查询操作排序,然后从头扫到尾,这样可以省时间。可用于把多维问题压掉一维处理。一般的思路想不出来的时候可以想想能不能离线,然后能不能扫。这里注意扫描线不一定扫时间或者坐标,数组下标也可能扫(见幻灯片习题5)。
主席树
这玩意叫可持久化线段树。它的实现原理就是每次对线段树进行操作,都只会对一条路径进行改变,那么我们不必建一棵新的线段树,只需要把没有改变的点复制下来,改变的改一下就可以了。这种数据结构比较耗空间,大概开30倍左右。
时隔经年(雾,我终于补上了主席树的板子……
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rint register int
#define inv inline void
#define ini inline int
#define maxn 200010
#define mid (l+r>>1)
using namespace std;
int cnt,rt[maxn],a[maxn],pos[maxn],rk[maxn];
struct node
{
int l,r,num;
}sum[maxn<<5];
ini cmp(int x,int y)
{
return a[x]<a[y];
}
//无比骚气的cmp
ini read()
{
rint c,r=0;
while (c<'0' || c>'9') c=getchar();
while (c>='0' && c<='9')
{
r=(r<<3)+(r<<1)+(c^48);
c=getchar();
}
return r;
}
inv insert(int &cur,int l,int r,int x)
{
sum[++cnt]=sum[cur];cur=cnt;//新建节点,复制信息
sum[cur].num++;
if (l==r) return;
if (x<=mid) insert(sum[cur].l,l,mid,x);
else insert(sum[cur].r,mid+1,r,x);
}
ini query(int t1,int t2,int l,int r,int k)
{
if (l==r) return l;
int t=sum[sum[t2].l].num-sum[sum[t1].l].num;
if (t>=k) return query(sum[t1].l,sum[t2].l,l,mid,k);
else return query(sum[t1].r,sum[t2].r,mid+1,r,k-t);
//感觉和FGT好像有木有
}
int main()
{
rint n,m;
n=read();m=read();
for (rint i=1;i<=n;i++) a[i]=read(),pos[i]=i;
sort(pos+1,pos+n+1,cmp);
for (rint i=1;i<=n;i++) rk[pos[i]]=i;
//离散化,因为值域比较大,建树的时候用排名来建树就行了
for (rint i=1;i<=n;i++)
{
rt[i]=rt[i-1];//复制上一个树的根的信息
insert(rt[i],1,n,rk[i]);
}
for (rint i=1;i<=m;i++)
{
rint l,r,k;
l=read();r=read();k=read();
rint ans=query(rt[l-1],rt[r],1,n,k);
//返回的是排名所以不能直接输出
printf("%d\n",a[pos[ans]]);
}
}
练习题
由于是团队题目,所以无法上链接,凑合着看图吧……
T1 子序列

这题还是很恶心的,不看ddd的题解根本做不出来…… 首先我们不考虑区间修改,只考虑第二问的暴力dp怎么办,可以想出方程 f[i][j] 表示到第i位以j结尾的本质不同的子序列的数量
if\quad (a[i]==0)\quad f[i][0]=f[i-1][0]+f[i-1][1]+1,f[i][1]=f[i-1][1]if(a[i]==0)f[i][0]=f[i−1][0]+f[i−1][1]+1,f[i][1]=f[i−1][1]if\quad (a[i]==1)\quad f[i][1]=f[i-1][0]+f[i-1][1]+1,f[i][0]=f[i-1][0]if(a[i]==1)f[i][1]=f[i−1][0]+f[i−1][1]+1,f[i][0]=f[i−1][0]
然后把它转化成矩阵乘法的形式,把某一位是0或1分别转化为两个01矩阵(这个代码里面有) 对于某个[f[i][0],f[i][1],1],就相当于原始矩阵[0,0,1]乘上一堆矩阵得到。 所以对于一个区间[l,r],我们可以把它中间的0和1转化为矩阵的形式,把这一堆矩阵乘起来,再乘以原始矩阵,最后然后得到的第一行第一列和第一行第二列加起来就OK了。 然后我们再看区间修改操作。这个ddd上课的时候有讲,对于一个3乘3的矩阵,把它的前两行和前两列交换一下,然后再和另一个交换过的矩阵相乘,得到的结果就是这两个矩阵相乘之后交换前两行和前两列。对于这个题来说,我们可以发现,代表0和1的两个矩阵,可以通过交换前两行和前两列来进行取反。那么这个题就可以做出来了。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define rint register int
#define inv inline void
#define inb inline bool
#define inl inline long long
#define ll long long
using namespace std;
struct martix
{
ll a[4][4];
martix() {memset(a,0,sizeof(a));}
};
martix t[100001],sum[400004],cs;
ll add[400004],big=1000000007,n,m;
inl read()
{
char c;ll r=0;
while (c<'0' || c>'9') c=getchar();
while (c>='0' && c<='9')
{
r=r*10+c-'0';
c=getchar();
}
return r;
}
inv pre(martix &k,ll x)
{
//代表0和1的矩阵在这里
if (!x)
{
k.a[1][1]=1;
k.a[2][1]=1;
k.a[2][2]=1;
k.a[3][1]=1;
k.a[3][3]=1;
}
else
{
k.a[1][1]=1;
k.a[1][2]=1;
k.a[2][2]=1;
k.a[3][2]=1;
k.a[3][3]=1;
}
}
martix jc(martix b,martix c)
{
martix d;
for (rint i=1;i<=3;i++)
for (rint j=1;j<=3;j++)
for (rint k=1;k<=3;k++)
d.a[i][j]=(d.a[i][j]+b.a[i][k]*c.a[k][j])%big;
return d;
}
inv change(martix &b)
{
for (rint i=1;i<=3;i++) swap(b.a[1][i],b.a[2][i]);
for (rint i=1;i<=3;i++) swap(b.a[i][1],b.a[i][2]);
}
inv build(ll l,ll r,ll num)
{
if (l==r)
{
sum[num]=t[l];
return;
}
ll mid=(l+r)>>1;
build(l,mid,num<<1);
build(mid+1,r,num<<1|1);
sum[num]=jc(sum[num<<1],sum[num<<1|1]);
}
inv pushdown(ll num)
{
if (add[num])
{
add[num<<1]^=1;
add[num<<1|1]^=1;
change(sum[num<<1]);
change(sum[num<<1|1]);
add[num]=0;
}
}
inv chadate(ll L,ll R,ll l,ll r,ll num)
{
if (L<=l && r<=R)
{
change(sum[num]);
add[num]^=1;
return;
}
ll mid=(l+r)>>1;
pushdown(num);
if (L<=mid) chadate(L,R,l,mid,num<<1);
if (R>mid) chadate(L,R,mid+1,r,num<<1|1);
sum[num]=jc(sum[num<<1],sum[num<<1|1]);
}
martix query(ll L,ll R,ll l,ll r,ll num)
{
if (L<=l && r<=R) return sum[num];
ll mid=(l+r)>>1;
pushdown(num);
martix ans;
if (L<=mid) ans=query(L,R,l,mid,num<<1);
if (R>mid)
{
if (L<=mid) ans=jc(ans,query(L,R,mid+1,r,num<<1|1));
else ans=query(L,R,mid+1,r,num<<1|1);
}
return ans;
}
int main()
{
n=read();m=read();
for (rint i=1;i<=n;i++)
{
ll x;x=read();
pre(t[i],x);
}
cs.a[1][3]=1;
build(1,n,1);
for (rint i=1;i<=m;i++)
{
ll opt,x,y;
opt=read();x=read();y=read();
if (opt==1) chadate(x,y,1,n,1);
if (opt==2)
{
martix answer;
answer=query(x,y,1,n,1);
answer=jc(cs,answer);
printf("%lld\n",(answer.a[1][1]+answer.a[1][2])%big);
}
}
}
T2 割草

这题简直TM毒瘤到爆……比第一道和第三道都难的存在。ddd讲课的时候就说过这题思路简单然而难以实现,我算是领教了。 想了半天想不出来,只能看题解了……题解也是真心难懂,要维护一堆东西。 细节的东西在代码里面有注释,那说一下大体思路吧。 因为收割不计较地的次序,所以我们可以先给它按照生长速度排个序,我们可以发现不管收割不收割,不管在哪个时间,生长速度快的总是最高的,这就有一个单调性。但我们这里不用扫描线,我们每次收割二分出高为b以上的,然后把它们割成b。答案就是割掉的那些。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define rint register int
#define inv inline void
#define inb inline bool
#define inl inline long long
#define ll long long
#define maxn 500001
using namespace std;
inl read()
{
char c;ll r=0;
while (c<'0' || c>'9') c=getchar();
while (c>='0' && c<='9')
{
r=r*10+c-'0';
c=getchar();
}
return r;
}
ll n,m;
ll a[maxn];//单位时间内生长速度
ll sum[maxn<<2];//某段区间内高度之和
ll grow[maxn<<2];//维护某段区间内生长速度的总和
ll flag[maxn<<2];//收割标记
ll flagd[maxn<<2];//上次收割的时间
ll lastd[maxn<<2];//上次结算的时间(结算不一定收割,但收割一定结算)
ll minn[maxn<<2];//区间内单个植物的最小高度
ll maxx[maxn<<2];//区间内单个植物的最大高度
inv build(ll l,ll r,ll num)
{
flag[num]=-1;
if (l==r)
{
grow[num]=a[l];
return;
}
int mid=(l+r)>>1;
build(l,mid,num<<1);
build(mid+1,r,num<<1|1);
grow[num]=grow[num<<1]+grow[num<<1|1];
//神TM智障的错误→→→→→→→↑↑
}
inv pushdown(ll ln,ll rn,ll num)
{
if (flag[num]>=0)//带有收割过的标记,就往下传递
{
flag[num<<1]=flag[num];
flag[num<<1|1]=flag[num];
sum[num<<1]=ln*flag[num];
sum[num<<1|1]=rn*flag[num];
minn[num<<1]=minn[num<<1|1]=maxx[num<<1]=maxx[num<<1|1]=flag[num];
flagd[num<<1]=flagd[num<<1|1]=flagd[num];
lastd[num<<1]=lastd[num<<1|1]=flagd[num];
//标记没有传递下来,两段子区间一定没有结算过
//但是当前区间num刚刚经过结算
//所以两段子区间的上次结算时间不应该是num的结算时间
//而是上次收割的时间
flag[num]=-1;
}
}
inl query(ll d,ll b,ll l,ll r,ll num)
{
ll ans;
ll timi=d-lastd[num];//距离上次结算的时间
sum[num]+=timi*grow[num];
minn[num]+=timi*a[l];
maxx[num]+=timi*a[r];
//是单个植物的最小/最大高度,所以要乘a[];由于a单调,取两端就行了
lastd[num]=d;//该区间已在该时间结算
if (maxx[num]<=b)//该区间不需收割
return 0;
if (minn[num]>b)//该区间必须收割
{
ans=sum[num]-(r-l+1)*b;
sum[num]=(r-l+1)*b;
minn[num]=maxx[num]=b;
flag[num]=b;
flagd[num]=d;
return ans;
}
//该区间有一部分需要收割
ll mid=(l+r)>>1;
pushdown(mid-l+1,r-mid,num);
ans=query(d,b,l,mid,num<<1)+query(d,b,mid+1,r,num<<1|1);
sum[num]=sum[num<<1]+sum[num<<1|1];
minn[num]=minn[num<<1];maxx[num]=maxx[num<<1|1];
return ans;
}
int main()
{
n=read();m=read();
for (rint i=1;i<=n;i++) a[i]=read();
sort(a+1,a+n+1);
build(1,n,1);
for (rint i=1;i<=m;i++)
{
ll d,b;
d=read();b=read();
printf("%lld\n",query(d,b,1,n,1));
}
}
T3 过年
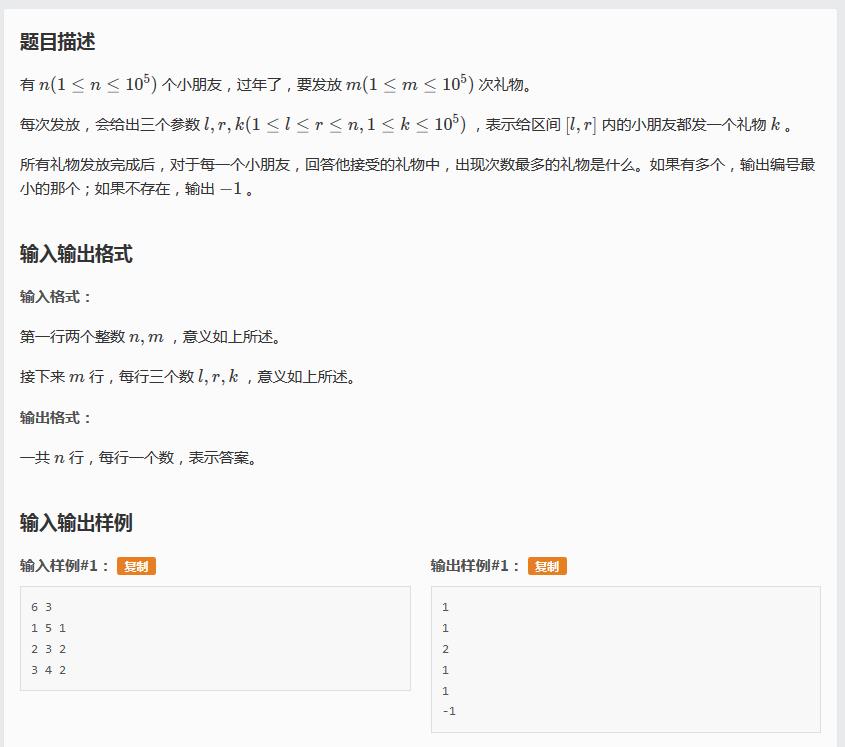
这道题我好像活活卡过去的?用时倒数第二,内存倒数第一?不过好像思路是对的…… 那就恬不知耻的说一下思路吧。 说一下建树,我们建立一个以礼物种类为区间的线段树,也就是说总区间是所有礼物种类,里面装的内容是最大值,也就说根节点装的就是最多的礼物出现次数。我们在里面封装pair,存两个值,一个礼物种类,一个出现次数,然后就可以不用查询,直接输出根节点的种类了。 再说一下细节。我们对于每一次送礼,都用差分进行操作。比如说我给从2到4的小朋友送种类为k的礼物,我们先在2上打个标记,在这里要单点修改一下,把k这个位置加1,在5(你没看错不是4)上面打个标记,在这里把k这个位置减1。这样操作之后,我们就可以用扫描线从下标1扫到n进行单点修改之后直接调用根节点了,是不是很机智(你TM建了40万个队列好意思说)?
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define rint register int
#define inv inline void
#define inb inline bool
#define ini inline int
using namespace std;
ini read()
{
char c;int r=0;
while (c<'0' || c>'9') c=getchar();
while (c>='0' && c<='9')
{
r=r*10+c-'0';
c=getchar();
}
return r;
}
int n,m;
struct node
{
pair<int,int> p;
};
struct sett
{
queue< pair<int,int> > q;
};
sett a[100005];
node sum[400004];
int add[400004];
inv pushup(int num)
{
pair<int,int> p1=sum[num<<1].p;
pair<int,int> p2=sum[num<<1|1].p;
if (p1.second>=p2.second) sum[num].p=p1;
else sum[num].p=p2;
}
inv pushdown(int num)
{
if (add[num])
{
add[num<<1]+=add[num];
add[num<<1|1]+=add[num];
sum[num<<1].p.second+=add[num];
sum[num<<1|1].p.second+=add[num];
add[num]=0;
}
}
inv build(int l,int r,int num)
{
if (l==r)
{
sum[num].p=make_pair(l,0);
return;
}
int mid=(l+r)>>1;
build(l,mid,num<<1);
build(mid+1,r,num<<1|1);
}
inv change(int x,int c,int l,int r,int num)
{
if (l==r)
{
sum[num].p.second+=c;
add[num]+=c;
return;
}
pushdown(num);
int mid=(l+r)>>1;
if (x<=mid) change(x,c,l,mid,num<<1);
if (x>mid) change(x,c,mid+1,r,num<<1|1);
pushup(num);
}
int main()
{
n=read();m=read();
build(1,n,1);
for (rint i=1;i<=m;i++)
{
int l,r,k;
l=read();r=read();k=read();
pair<int,int> p1=make_pair(1,k);
pair<int,int> p2=make_pair(-1,k);
a[l].q.push(p1);
a[r+1].q.push(p2);
}
for (rint i=1;i<=n;i++)
{
while (!a[i].q.empty())
{
pair<int,int> now=a[i].q.front();
int x=now.first;
int y=now.second;
a[i].q.pop();
change(y,x,1,n,1);
}
int answer;
if (!sum[1].p.second) answer=-1;
else answer=sum[1].p.first;
printf("%d\n",answer);
}
}


