这一天东西好多啊
SX-D2
Trie树
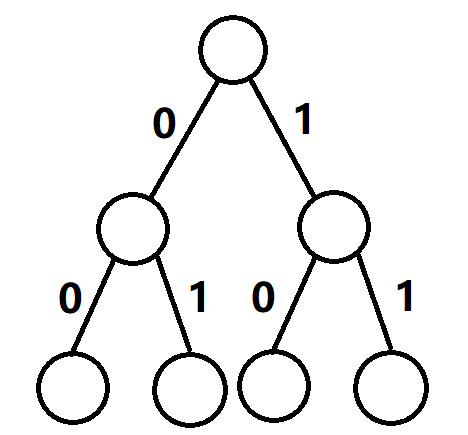
01 trie有查找的功能,它的每一层代表二进制的每一位,一条路径就代表一个数。当然我们可以用这种数据结构来处理某个数列异或后的查找,比如说找数列中异或起来最大的,或者说异或之后的mex(最小非负整数),具体看题目分析。
01trie
平衡树
这里ddd没有讲treap也没有讲splay,而是讲了一种lxl自创的平衡树,能够支持treap和splay的操作,被广大人民群众命名为宗法树。这里我们从头讲起。
平衡树支持什么操作?
平衡树在维护一个有序的序列
插入x
删除x
查询x的排名
查询排名为x的数
查询x的前驱和后继
使这些操作的复杂度在(log n)左右
二叉查找树
平衡树实现的基础是二叉查找树。
二叉查找树是一种二叉树,对于树上的每一个非叶子节点,都满足它的左子树都小于它,它的右子树都大于它。
删除某个节点的时候并不真正把它删掉,而是做一个标记,查到它的时候忽略它就可以了。
查询某个数的排名的时候,每次往右递归,都加上当前左子树的大小+1(包括当前节点),最后再+1(自己的排名等于自己前面的数量+1)。
查询排名为x的某个数的时候,每次都看它加上它的左子树够不够x,如果够就向左,不够的话用x减去(左子树+1),向右递归,直到自己就是要找的数。
查询前驱和后继就可以利用前面两种操作,先查出自己的排名,然后查排名为自己+1和自己-1的数。
宗法树
宗法树模型
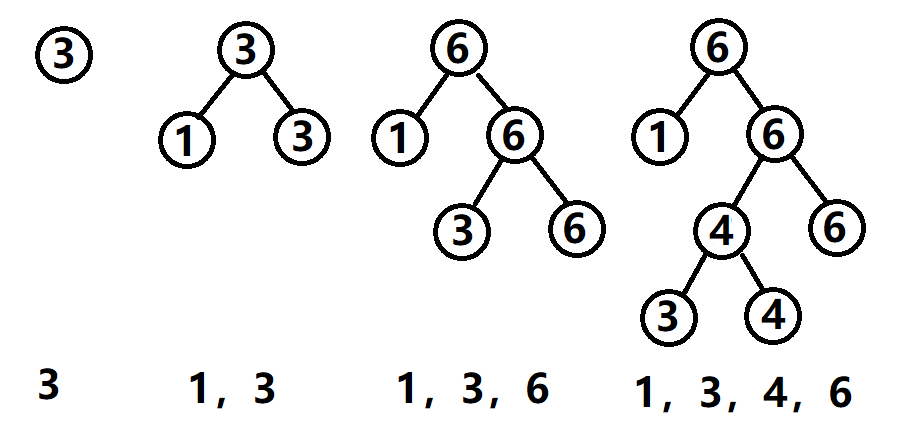
这个树的确属于平衡树,但它也是一种特殊的线段树。它满足以下几条性质:
- 只有叶子节点表示真正的信息
- 非叶子节点维护叶子节点的最值或其它信息。在名次树中,它等于自己右儿子的值。
- 插入或删除某个点的时候,从根向下走,直到叶子。
- 名次树中叶子节点具有单调性。
插入
从根向下递归,直到找到第一个比x大的最小的的叶子节点。 每次插入都要新建两个新节点。
inv pushup(int cur) { if (!size[ls[cur]]) return; //宗法树左子树为空,右子树就为空,当前就是叶子节点,直接退出即可 size[cur]=size[ls[cur]]+size[rs[cur]]; val[cur]=val[rs[cur]]; } inv insert(int cur,int x) { if (size[cur]==1)//到达叶子节点 { ls[cur]=newnode(min(x,val[cur])); rs[cur]=newnode(max(x,val[cur])); pushup(cur); //新建左右儿子,向上更新父亲节点 return; } maintain(cur); if (x>val[ls[cur]]) insert(rs[cur],x); //x比左边的都要大,就在右边,反之在左边 //zz错误↑ else insert(ls[cur],x); pushup(cur); }删除
从根向下找到要删除的点,然后向上pushup即可。
inv copynode(int cur,int pre) { size[cur]=size[pre]; val[cur]=val[pre]; ls[cur]=ls[pre]; rs[cur]=rs[pre]; } inv erase(int cur,int x,int fa) { if (size[cur]==1)//到达叶子节点 { if (cur==ls[fa]) cur=rs[fa]; else cur=ls[fa]; copynode(fa,cur); //如果要删去左儿子,父亲就变成右儿子;反之同理 return; } maintain(cur); int next; if (x>val[ls[cur]]) next=rs[cur]; else next=ls[cur];//x比左边的都要大,就在右边,反之在左边 erase(next,x,cur); pushup(cur); }查询x的排名
对于当前节点,它的左儿子代表它左子树中最大的值,那么如果要查询的值比左儿子大,那就向右递归,然后把答案加上左子树的大小;如果要查询的值小于等于左儿子,就往左递归,不用加名次了,一直递归到叶子节点,累加得到的就是比要查询的小的个数。
一个细节,如果查询一个比树上最大值还大的数的排名,到叶子节点要return 2,因为你实际查询到的是树上最大值,但你要查一个比最大值还大的,名次就要+1。ini rank(int cur,int x)//查询x的排名 { if (size[cur]==1) return 1;//自己的排名=比自己小的+1 maintain(cur); if (x>val[ls[cur]]) return rank(rs[cur],x)+size[ls[cur]]; else return rank(ls[cur],x); }查询排名为x的数
和二叉查找树基本相同,一直递归到叶子节点即可。
ini kth(int cur,int x)//查询排名为x的数 { if (size[cur]==x) return val[cur];//当前子树中有x个数,就找到了,返回当前子树根的值 maintain(cur); if (x>size[ls[cur]]) return kth(rs[cur],x-size[ls[cur]]); //如果x大于左子树中数的数量,就在右子树中寻找排名为(x-左子树大小)的点 else return kth(ls[cur],x); }旋转
当你发现左右两边中一边较高而另一边较低的时候,由于宗法树只有叶子节点维护真正信息,只要保证宗法树的叶子顺序不变,而进行更换父节点操作,然后pushup一下,树的性质不会变,旋转只是一个意象的表达而已,实际上就是换父节点。这个复杂度证明比较复杂,但是可证复杂度(log n)。
关于什么时候旋转,大概在一边为另一边的4~5倍时就转。ini merge(int l,int r)//left_son,right_son { int cur; if (numt) cur=trash[numt--]; else cur=++numz; //垃圾回收 size[cur]=size[l]+size[r]; val[cur]=val[r]; ls[cur]=l;rs[cur]=r; return cur; } inv rotate(int cur,bool flag) { if (!flag)//左右变右左 { rs[cur]=merge(rs[ls[cur]],rs[cur]); //右自变右右,左右变右左 trash[++numt]=ls[cur]; //左自废掉了,扔进回收站 ls[cur]=ls[ls[cur]]; //左左变左自 } else//右左变左右 { ls[cur]=merge(ls[cur],ls[rs[cur]]); trash[++numt]=rs[cur]; rs[cur]=rs[rs[cur]]; } } inv maintain(int cur) { if (size[ls[cur]]>size[rs[cur]]*5) rotate(cur,0);//左沉,左右变右左 else if (size[rs[cur]]>size[ls[cur]]*5) rotate(cur,1);//右沉,右左变左右 if (size[ls[cur]]>size[rs[cur]]*5) rotate(ls[cur],1),rotate(cur,0); //换完仍然左边沉,必是左右沉,左右分半给左左,剩下变右左 else if (size[rs[cur]]>size[ls[cur]]*5) rotate(rs[cur],0),rotate(cur,1); //换完仍然右边沉,必是右左沉,右左分半给右右,剩下变左右 }垃圾回收
旋转的时候由于既新建一个节点,又删除一个节点,所以应该进行垃圾回收,把删掉的点重新利用,不然会造成节点浪费(
我在说什么)?!ini newnode(int v) { int cur;//新建一个节点 if (numt) cur=trash[numt--]; else cur=++numz; //如果回收站里面有点,就用上,没有就加点 size[cur]=1; val[cur]=v; ls[cur]=rs[cur]=0; //如果是回收站里面的,它的左右子树可能会不是0 return cur; }主程序
//题目 luogu3369 普通平衡树 int main() { scanf("%d",&n); root=newnode(big); //先建一个特别大的根节点,方便加点 for (rint i=1;i<=n;i++) { int opt,x; opt=read();x=read(); if (opt==1) insert(root,x); if (opt==2) erase(root,x,root); if (opt==3) printf("%d\n",rank(root,x)); if (opt==4) printf("%d\n",kth(root,x)); if (opt==5) printf("%d\n",kth(root,rank(root,x)-1)); if (opt==6) printf("%d\n",kth(root,rank(root,x+1))); // zz错误之二 ↑↑ //对于查询一个并不在树中的节点的排名,我们会返回比它大的最小的点的排名 //如果它就在树中,就会返回它在树中的排名 //所以不管节点在不在树中,我们都会返回它的正确排名 //所以查x的前驱的话直接查询(rankx-1)的数是谁是没有问题的 //但是如果查后继的话,就要分情况讨论 //如果点x就在树中,我们就要查询排名(rankx+1)的数 //但是如果不在,我们就要查询排名(rankx)的数(比x大的最小的点,就是后继) //这时候就可以骚操作,查询rank(x+1)的数,这样不管x在不在树中,都会直接返回后继 } }关于可并堆
我们知道宗法树可以实现堆的功能,所以对于两个宗法树维护的堆,我们可以通过新建一个根节点进行合并。因为我们要的是一个堆,就不需要维护顺序了,只需要维护最大最小值就行了。
树套树
树套树的作用
我们知道,二维数点可以用线段树静态实现,但是如果有一个不断加点不断查询的二维数点,而且强制在线,该怎么做?
PS:二维数点一定要想到前缀性。 最好的答案当然是树套树。
这并不是一种数据结构,而是一种思想。一棵树套树,外层是一棵树,外层的每个节点的内层也是一棵树,这就叫树套树。线段树套线段树
我们有两层线段树,外层维护x轴,内层维护y轴,外层线段树的值维护的是内层线段树的根在哪里,内层的线段树和一般的线段树一样。外层线段树要先建好,然后内层要动态开点,不然会空间不够。每次操作会经过外层(log n)个节点,然后再经过内层(log n)个节点,单次操作的复杂度为(log2 n)。
数组版动态开点,要建两个数组,来维护某个点的左右儿子,如果是空的的话就开点。
因为在内层开点没有办法pushup,所以要从根节点开始一直到加点的外层线段树的节点每一层都开一个内层点。
这个东西就是单点修改,区间的修改似乎不可做。
做法:先查外层,对于每个外层进行查内层。
查询到一个没有开过的点直接返回0。
如果数据奇大外层也要动态开点。线段树套平衡树
本质一样,外层线段树维护内层平衡树的根,内层的平衡树就是普通的平衡树。二维数点就是y2的rank减去y1-1的rank,就是y1~y2之间的值了。
当然,两种树套树也都可以做二维的区间最值。
例题:luogu 3380 二逼平衡树比较两种树套树
线段树套线段树好写,而且是完全平衡的,常数相对小。但是复杂度是(log2 n)的。 线段树套平衡树不能做到理论上的完全平衡,但是由于平衡树加点只加一个,所以复杂度是(log n)。
具体看情况灵活选择。轻重链剖分
其实就是俗称的树链剖分。
PS:树链剖分不止有轻重链剖分。但是大多数时候的树链剖分指的就是轻重链剖分。dfs序
给树的节点重新编号,使得任意一个节点满足子树的dfs序都比它要大,而且它子树的dfs序是一段连续的区间。
轻重链剖分的性质
一种特殊的dfs序。
满足每个节点的子树dfs序是一段连续的区间。
满足树上的任意一条路径最多是由logn段连续的区间构成,就是说树链剖分剖出来的序就是满足这样一个性质,可以把对于路径的操作拆成对O(log n)段线性的序列的操作,进而可以用数据结构来维护。如何进行轻重链剖分?
对树进行深度优先遍历,得到每个节点的重儿子,即它的儿子中子树节点最多的一个。再一次进行深度优先遍历,优先访问重儿子。这样遍历过的树能够满足以上性质。 对于路径(x,y)的操作,我们一般要去找这两点所在的连续的一段的最顶端是哪个节点。我们把x设为段头深度较深的那一个(就是客观高度比较矮),然后跳上去找y的段头,这个段头用top数组在第二遍dfs时记录。top即当前点最高到哪个点能够成一条dfs序连续的路径。然后不断上跳到段头,直到跳到一条重链上(top值不一样即不在同一条重链上)。
轻重链剖分能干什么?
序列转化:把树上的路径转化为区间,如上。
求LCA(思路跟求xy的重链相似)
求LA(在logn的复杂度内查询x的深度为d的祖先是谁):倍增可做,但树链剖分也可以做。这里注意,不是向上走深度为d的祖先,而是客观深度为d的祖先是谁。先看当前点的top是不是比d还深,如果是的话跳到top的父亲,直到跳到x和这个深度为d的祖先在同一条重链上,即它们的dfs序是连续的,所以这时我们就可以列出公式deep[x]-deep[y]=dfn[x]-dfn[y]。所以在第二遍dfs我们要记录一下idfn,即dfn的映射,即idfn[dfn[y]]=y,我们最终得到的值就是idfn[d-deep[x]+dfn[x]]。luogu3384 树链剖分
注释内容是我犯过的那些脑残错误……
#include<iostream> #include<cstdio> #include<cstring> #define rint register int #define inv inline void #define ini inline int #define mid (l+r>>1) #define ls (num<<1) #define rs (num<<1|1) #define maxn 200020 using namespace std; int n,m,rt,mod,cnt,dfn_clock; int a[maxn],tot[maxn],f[maxn],head[maxn],deep[maxn],sum[maxn<<2],add[maxn<<2],top[maxn],dfn[maxn],son[maxn],idfn[maxn]; ini read() { char c;int r=0,f=1; while (c<'0' || c>'9') { if (c=='-') f=-1; c=getchar(); } while (c>='0' && c<='9') { r=r*10+c-'0'; c=getchar(); } return r*f; } struct node { int next,to; }ljb[maxn]; //因为要建双向边,所以maxn应该是n的两倍 inv add_edge(int x,int y) { ljb[++cnt].next=head[x]; ljb[cnt].to=y; head[x]=cnt; } inv dfs1(int x,int dep,int fa) { deep[x]=dep; f[x]=fa; tot[x]=1; int maxx=-1; for (rint i=head[x];i;i=ljb[i].next) { int y=ljb[i].to; if (y!=fa) { dfs1(y,dep+1,x); tot[x]+=tot[y]; if (tot[y]>maxx) { maxx=tot[y]; son[x]=y; } } } } inv dfs2(int x,int tp) { dfn[x]=++dfn_clock; idfn[dfn_clock]=x; top[x]=tp; if (!son[x]) return; dfs2(son[x],tp); for (rint i=head[x];i;i=ljb[i].next) { int y=ljb[i].to; if (y!=f[x] && y!=son[x]) dfs2(y,y); } } inv pushdown(int num,int ln,int rn) { if (add[num]) { add[ls]+=add[num]; add[rs]+=add[num]; sum[ls]=(sum[ls]+ln*add[num])%mod; sum[rs]=(sum[rs]+rn*add[num])%mod; //此处不是仅仅加上add[num]就可以的 //别忘了%mod add[num]=0; } } inv build(int l,int r,int num) { if (l==r) { sum[num]=a[idfn[l]]%mod; //idfn保存dfs序对应的本来的数字 //这里建树是针对第二遍的dfs序 //因为只有第二遍dfs序才能把路径转成区间 return; } build(l,mid,ls); build(mid+1,r,rs); sum[num]=(sum[ls]+sum[rs])%mod; } inv change(int L,int R,int l,int r,int x,int num) { if (L<=l && r<=R) { sum[num]+=(r-l+1)*x; add[num]+=x; return; } pushdown(num,mid-l+1,r-mid); //zz错误→→→↑↑ if (L<=mid) change(L,R,l,mid,x,ls); if (R>mid) change(L,R,mid+1,r,x,rs); //大写L和R sum[num]=(sum[ls]+sum[rs])%mod; } ini query(int L,int R,int l,int r,int num) { if (L<=l && r<=R) return sum[num]%mod; pushdown(num,mid-l+1,r-mid); int ans=0; if (L<=mid) ans=(ans+query(L,R,l,mid,ls))%mod; if (R>mid) ans=(ans+query(L,R,mid+1,r,rs))%mod; return ans; } inv treeadd(int x,int y,int C) { C%=mod; int t1=top[x]; int t2=top[y]; int ans=0; while (t1!=t2) { if (deep[t1]<deep[t2]) { swap(x,y); swap(t1,t2); } //这里和lca不一样,lca是低的往高的上面跳,直到跳到同一深度 //这个是不断交替上跳 change(dfn[t1],dfn[x],1,n,C,1); x=f[t1]; t1=top[x]; } if (deep[x]>deep[y]) swap(x,y); change(dfn[x],dfn[y],1,n,C,1); } ini treeques(int x,int y) { int t1=top[x]; int t2=top[y]; int ans=0; while (t1!=t2) { if (deep[t1]<deep[t2]) { swap(x,y); swap(t1,t2); } ans=(ans+query(dfn[t1],dfn[x],1,n,1))%mod; x=f[t1]; t1=top[x]; } if (deep[x]>deep[y]) swap(x,y); ans=(ans+query(dfn[x],dfn[y],1,n,1))%mod; return ans; } int main() { n=read();m=read();rt=read();mod=read(); for (rint i=1;i<=n;i++) a[i]=read(); for (rint i=1;i<=n-1;i++) { int x,y; x=read();y=read(); add_edge(x,y); add_edge(y,x); } dfs1(rt,1,rt); dfs2(rt,rt); build(1,n,1); for (rint i=1;i<=m;i++) { int opt,x,y,z; opt=read(); if (opt==1) { x=read();y=read();z=read(); treeadd(x,y,z); } if (opt==2) { x=read();y=read(); printf("%d\n",treeques(x,y)); } if (opt==3) { x=read();z=read(); change(dfn[x],dfn[x]+tot[x]-1,1,n,z,1); } if (opt==4) { x=read(); printf("%d\n",query(dfn[x],dfn[x]+tot[x]-1,1,n,1)); //这里是dfn[x]而不是x } } }其他
单调队列
LCT
点分治
莫队
分块

