这讲师 简直了
luogu春令营 D4
根号平衡
那是啥?
有x次修改,单次复杂度为O(a)。
有y=kx次查询,单次复杂度为O(b)。
在满足一定条件的题里面,可以通过提高其中一边的复杂度,降低另一边的复杂度来达到更好的效果。
这时满足xa=kxb。
举个栗子?
就拿线段树来举例,如果不用线段树,修改是O(1),查询是O(n),一共有m次操作。
这时候你用线段树,把修改和查询都平衡成log n,就降低了整体的复杂度。
我们知道如果有一个长度为n的序列,把它分成满x叉树的形式,那么有logx(n)层。
线段树就是一个满二叉树,所以它有log(n)层。
而运用根号平衡的分块算法就是把两边都平衡为O(sqrt(n)),也就是建立一个sqrt(n)叉树,这棵树只有两层(算上根节点三层)。
分块
分块主要分为静态分块和动态分块。
静态分块指的是放一些关键点,预处理关键点到关键点的信息来加速查询的,不能支持修改。
目前认为:如果可以离线,静态分块是莫队算法的子集。
动态分块就是把序列分块,每块维护信息,支持修改。下面的分块指动态分块。
分块基础
要实现区间加,区间和,我们可以把sqrt(n)个元素放在一块维护。
我们一般把每次操作完整覆盖的块定义为”整块”,而没有完整覆盖的块定义为”零散块”。

每次操作最多经过O(sqrt(n))个整块,最多2个零散块
分块的本质就是一个sqrt(n)叉树,第一层一个节点,第二层sqrt(n)个节点,第三层n个节点
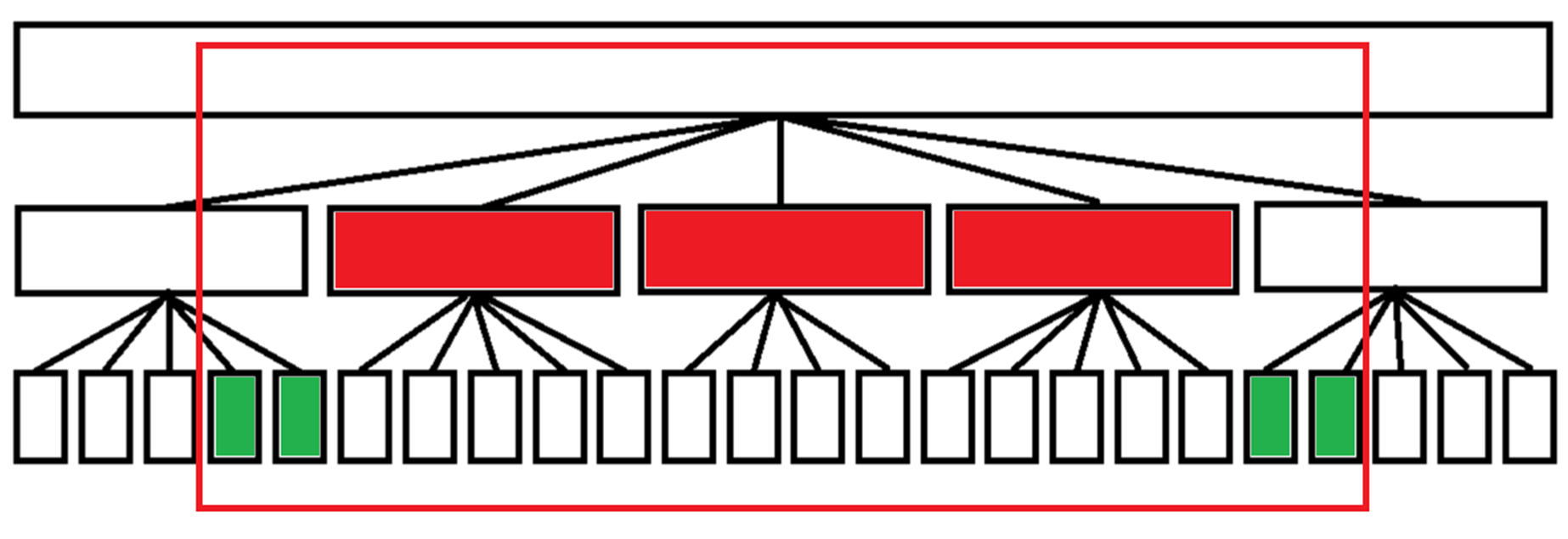
对于上图的这个玩意,修改的时候整块打标记,零散块枚举+排序重构
block -> 块大小
belong[i] -> i属于的块编号
l[i] -> 第i块的左端点
r[i] -> 第i块的右端点
for( register int i = 1 ; i <= n ; i++ ) belong[i] = ( i - 1 ) / block;
for( register int i = 1 ; i <= n ; i++ )
if( !l[ belong[i] ] )
l[ belong[i] ] = i;
for( register int i = n ; i ; i-- )
if( !r[ belong[i] ] )
r[ belong[i] ] = i;
modify/find( int L , int R )//修改、查询
if( belong[l] == belong[r] )
for( register int i = L ; i <= R ; i++ )
......
else
{
for( register int i = L ; i <= r[ belong[L] ] ; i++ )
......
for( register int i = l[ belong[R] ] ; i <= R ; i++ )
......
for( register int i = belong[L] + 1 ; i <= belong[R] - 1 ; i++ )
......
那么我们再看一个例题,如果要区间加,然后求区间内小于x的数
修改同上,查询整块时,如果整块上带着标记y,那么就二分查找小于x-y的数,零散块直接暴力查询即可。
让我们来分析一下复杂度
序列长度为n,第二层x个块
修改:
整块O(1) 直接标记即可
零散块O(n/x) 这里按照最劣情况来计算,n/x为块的大小
查询:
整块 O(log(n/x)) 二分查找
零散块O(n/x) 暴力枚举每一块
这里要知道,分块的块大小不一定是sqrt(n),具体是要靠根号平衡来算的,让我们试一下
毒瘤非说平衡出来是sqrt(n log n),但是我们算的都是n/2……
下一个题暂且先当做sqrt(n log n)来
把求区间小于x的数改成求区间第k小,然后还用上一题的方法如何?
这样的复杂度就是O(m sqrt(n log n) logv),被毒瘤卡掉了(尽管我并不知道他这复杂度哪来的
这里我们把块大小设为sqrt(n)logn
查询的时候进行二分答案,在整块上和零散块上分别计算,然后看看够不够k-1个就行了
我们有n个小块,块大小为sqrt(n) logn,所以整块的数量撑死为sqrt(n)/log n,零散块撑死为sqrt(n) logn,整块部分查询复杂度为单次O(log (sqrt(n)logn)),零散块查询复杂度为O(sqrt(n)log n),再暴力零散块时间堪忧。
这里我们把零散的两个块先归并成一个假的块,然后在这里面进行二分
知道这样能提升速度就行,具体复杂度,呵呵,我再信毒瘤就鬼了……
根号平衡的应用
O(1)单点修改,O(sqrt(n))区间和
直接分块,妥妥的。
O(sqrt(n))单点修改,O(1)区间和
中间一层维护块外前缀和,最底下一层维护块内前缀和,查询只需调用单点和其对应的分块,修改就要修改该分块内后面的单点,以及后面的分块的前缀和。
O(sqrt(n))区间加,O(1)查单点
又是裸分块,不解释。
O(1)区间加,O(sqrt(n))查单点
前缀和+查分。对于区间[l,r],给l-1,r和其所在分块打标记,l-1打减标记,r打加标记,然后每次查询只查该点以及它的块中它后面的点,还有它后面的块即可。
O(1)插入一个数,O(sqrt(n))查询第k小
先离散化之后,对值域进行分块,单点修改,每个块保存有几个数,查询的时候从头开始往后跑,直到数够了为止。
O(sqrt(n))插入一个数,O(1)查询第k小
这个玩意?自己真不大能想出来……
毒瘤的课实在难懂,只能看看fym大佬的解法
钻研了好久终于懂了……
这个题还是值域分块,只不过对于每个块,我们要维护的是一个OV(有序表)。
对于每个块,我们都维护l[i]和r[i],表示这个块里面有第l[i]~r[i]名的元素
先说一下比较简单的查询,我们维护belong[i]表示第[i]名在哪个块
然后直接O(1)调用
vec[belong[k]][k-l[belong[k]]]
即可。
我们再看一下插入。
先离散一下原序列的数和要插入的数,然后值域分块,经过这样的预处理,我们可以保证每次插入都绝对会插入到这个点最后应该所在的位置,所以,每次插入只需要在块内重构+改变后面块的l和r,这就OK了。
分块例题:教主的魔法
莫队
简单莫队算法
假设我们可以O(x)插入或删除一个元素
那么对于已知区间[l,r],我们可以O(x)得到[l-1,r],[l+1,r],[l,r-1],[l,r+1]
那么对于两个区间[l1,r1],[l2,r2]
如果把这俩看做平面上的坐标,那么我们可以用这俩的曼哈顿距离abs*(l1-l2)+abs(r1-r2)(不是欧氏距离)
我们可以O(x*(abs(l1-l2)+abs(r1-r2)))由[l1,r1]得到[l2,r2]
这就是简单莫队算法的本质
莫队是一个必须离线的算法,如果强制在线就无能为力了
如果序列长n,有m个询问,我们可以用一种特殊的顺序依次处理每个询问,使sigma在一个可以接受的范围内。我们通常是对序列分块,然后把询问排序,排序的时候以左端点所在块编号为第一关键字,右端点所在块编号为第二关键字。
这样排序的复杂度是O(nsqrt(m))
普通莫队是可以进行大力卡常数的,这里毒瘤主要给了两个技巧:
- 排序按照奇偶分别排,虽然玄学但是可以快一倍
inb cmp (node a,node b)
{
if (belong[a.l]^belong[b.l]) return belong[a.l]<belong[b.l];
if (belong[a.l]&1) return a.r<b.r;
return a.r>b.r;
}
- 调一下块的大小,同玄学,可以快10%左右
block=n/sqrt(m*2/3);
板子题:小Z的袜子

